Tidal Forces & Roche Limits
Interactive simulation of gravitational gradients and planetary disruption
Loading Tidal Forces Simulation...
Tidal Forces & Roche Limit
RRoche = 2.44 × Rprimary × (ρprimary/ρsatellite)1/3
Roche Limit: 2.44 R
Stress Ratio: 0.00
Safe Zone: Green
Stress Ratio: 0.00
Safe Zone: Green
Tidal Bulge
Tidal Bulge Height: 0.00 m
Tidal Acceleration: 0.00 m/s²
Force Differential: 0.00 N/kg
Safe Zone: Green | Danger Zone: Red
Tidal Bulge Height: 0.00 m
Tidal Acceleration: 0.00 m/s²
Force Differential: 0.00 N/kg
Satellite Status
Self-Gravity: 9.81 m/s²
Tidal Stress: 0.00 Pa
Stable Orbit
Distance Ratio: 1.02 × RRocheSelf-Gravity: 9.81 m/s²
Tidal Stress: 0.00 Pa
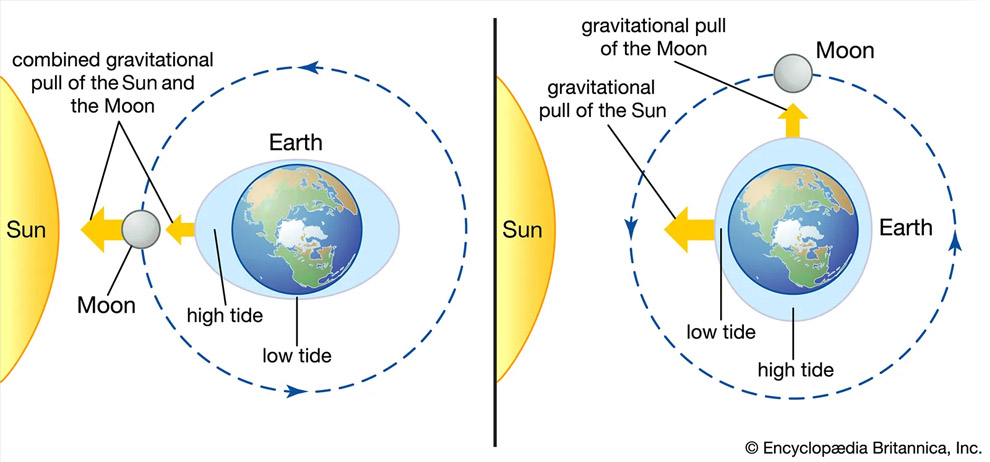
Gravitational Gradients
Tidal forces occur because gravity weakens with distance, creating a difference in gravitational pull across an extended body. This stretching force creates tidal bulges and can tear objects apart inside the Roche limit.
Tidal Locking
Many moons show the same face to their planet due to tidal forces slowing their rotation.
Roche Limit
The minimum distance where a satellite's self-gravity can withstand tidal disruption.
Tidal Heating
Io's volcanic activity and Europa's subsurface ocean are powered by tidal friction.
Real-World Examples
Earth-Moon
Tidal bulge: ~0.5 m
Orbit slowly expanding
Jupiter-Io
Intense tidal heating
Most volcanically active body
Saturn's Rings
Formed inside Roche limit
Particles cannot coalesce
Comet Shoemaker-Levy 9
Tidally disrupted by Jupiter
Collided as multiple fragments

